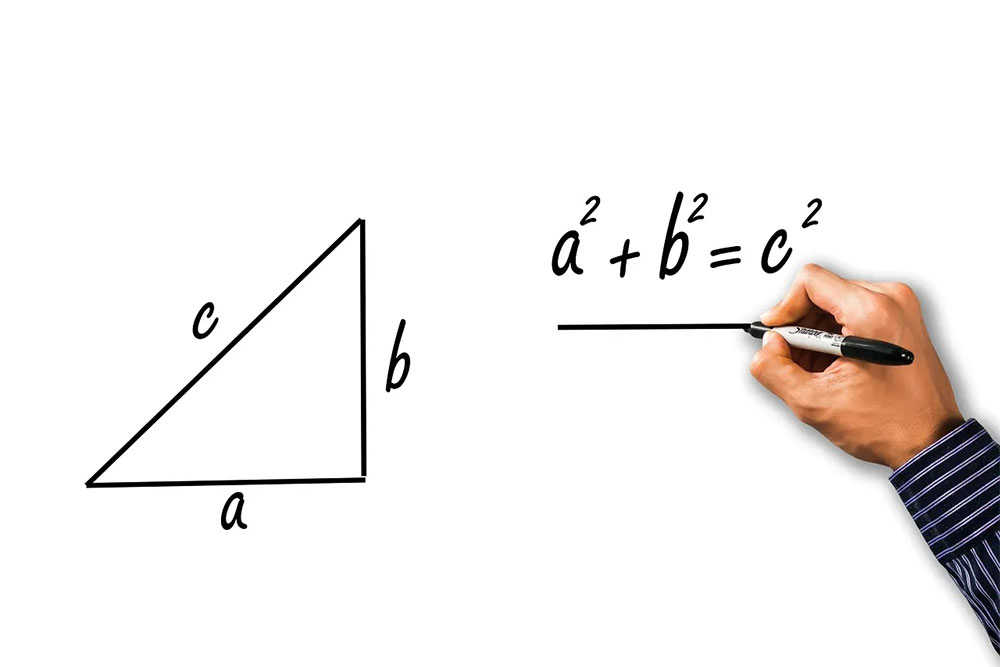Прямокутний трикутник — це трикутник, у якого один із кутів є прямим, тобто рівним 90 градусам. У прямокутному трикутнику можна виділити три основні сторони: два катети та гіпотенузу.
- Катети: Це дві сторони прямокутного трикутника, які утворюють прямий кут. Позначаються як a та b. Катети завжди перпендикулярні одна одній і лежать при прямому вугіллі.
- Гіпотенуза: Це найдовша сторона прямокутного трикутника, що знаходиться навпроти прямого кута. Позначається як с. Гіпотенуза є гіпотенузою у сенсі теореми Піфагора, яка стверджує, що квадрат гіпотенузи дорівнює сумі квадратів катетів.
Теорема Піфагора та знаходження катета
Теорема Піфагора виражається так:
c2 = a2 + b2
Де:
- c – довжина гіпотенузи
- a та b – довжини катетів
Таким чином, для знаходження катета у прямокутному трикутнику, якщо відомі довжини гіпотенузи та одного з катетів, можна скористатися теоремою Піфагора для знаходження довжини іншого катета.
Допустимо, у нас є прямокутний трикутник зі сторонами a = 3 і c = 5, і ми хочемо знайти довжину другого катета b.
Застосовуючи теорему Піфагора, ми отримуємо:
b2 = c2 − a2
b2 = 52 − 32
b2 = 25 − 9
b2 = 16
Таким чином, квадрат довжини другого катета b дорівнює 16. Щоб знайти сам катет b, потрібно витягти квадратний корінь із 16:
b = √16
b = 4
Таким чином, другий катет у цьому прикладі дорівнює 4.
Теорема Піфагора є одним із основних інструментів для роботи з прямокутними трикутниками і дозволяє знаходити довжини сторін, якщо відомі довжини інших сторін трикутника.