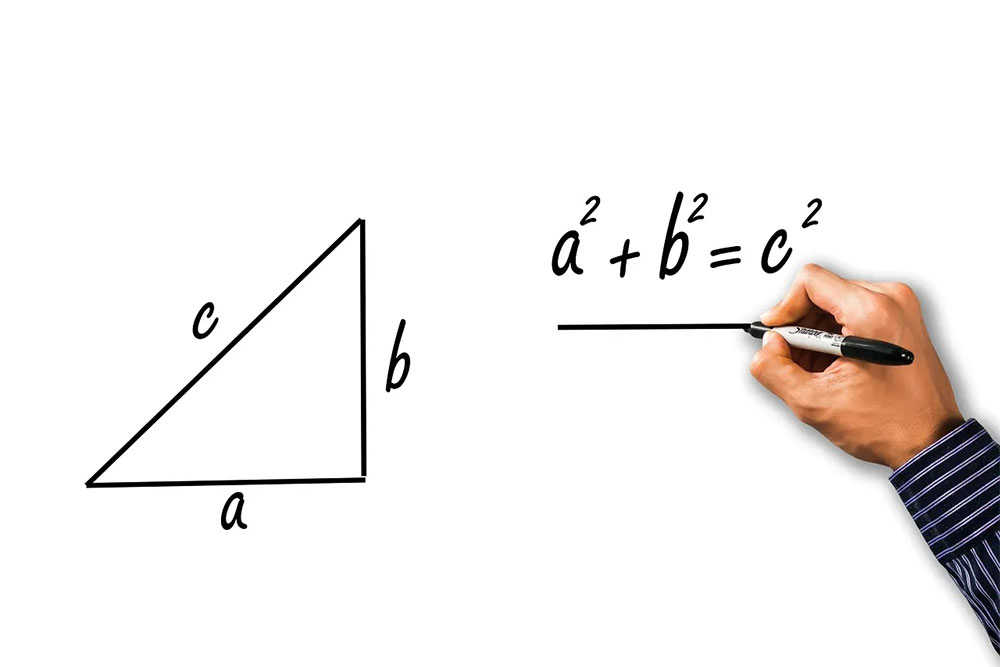Прямоугольный треугольник — это треугольник, у которого один из углов является прямым, то есть равным 90 градусам. В прямоугольном треугольнике можно выделить три основных стороны: два катета и гипотенузу.
- Катеты: Это две стороны прямоугольного треугольника, которые образуют прямой угол. Обозначаются как a и b. Катеты всегда перпендикулярны друг другу и лежат при прямом угле.
- Гипотенуза: Это самая длинная сторона прямоугольного треугольника, которая находится напротив прямого угла. Обозначается как c. Гипотенуза является гипотенузой в смысле теоремы Пифагора, которая утверждает, что квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора и нахождение катета
Теорема Пифагора выражается следующим образом:
c2 = a2 + b2
Где:
- c — длина гипотенузы
- a и b — длины катетов
Таким образом, для нахождения катета в прямоугольном треугольнике, если известны длины гипотенузы и одного из катетов, можно воспользоваться теоремой Пифагора для нахождения длины другого катета.
Допустим, у нас есть прямоугольный треугольник со сторонами a = 3 и c = 5, и мы хотим найти длину второго катета b.
Применяя теорему Пифагора, мы получаем:
b2 = c2 − a2
b2 = 52 − 32
b2 = 25 − 9
b2 = 16
Таким образом, квадрат длины второго катета b равен 16. Чтобы найти сам катет b, нужно извлечь квадратный корень из 16:
b = √16
b = 4
Таким образом, второй катет в данном примере равен 4.
Теорема Пифагора является одним из основных инструментов для работы с прямоугольными треугольниками и позволяет находить длины сторон, если известны длины других сторон треугольника.